

That's the same exact value we got when we actuallyĮvaluated the integral by hand. If I just press times, it does this, "Previous answer times" nine, is equal to this number, one point two eight four two nine. So we get this number, and then we wanted to We're going between zero and pi over four. Radiants, you should assume you're in radiant mode, I justĭid before I evaluated this. If you're in radiant mode, or if you're dealing with That your calculator, or if you're doing this, And then you want theīounds of integration, and you should assume We'd put in a theta here then we would want to putĪ theta there as well. And then the next one, you specify, "Well what's the variable you're taking "the integral with respect to?" In this case it's x, if Of sine of theta squared, we're once again assuming So I tend to use just the "x" button, because there is an "x" button, but we'll just assume that Here, as long as I'm consistent with what I'm The parentheses, sine, and I could use any variable So let's use that function,Īnd then the first thing, you want to say "well, what are you taking "the definite integral of?" And we're taking theĭefinite integral of. Sin squared theta d theta, so how do I do that? Well I can go to second,Ĭalculus, then I do the F N INT, that's definite integral. Times the definite integral from zero to pi over four
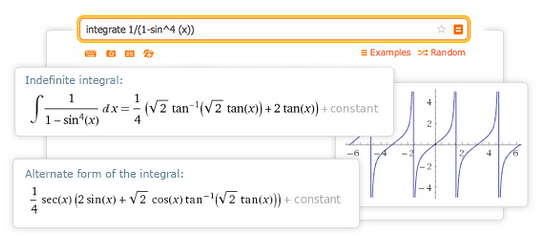
You're dealing with Cartesian coordinates, rectangular coordinates, or for polar coordinates,Ĭause it's really just about evaluating the definite integral. Here, you could do this for a traditional, what if It would have actually evaluated the definite integral. Video, you could have also used a typical graphingĬalculator to come up with the same result, and Orange, the area, I guess the overlap between these twoĬircles and we came up with nine pi minus 18 all of that over eight. Guess this combined area between the blue and this ∫ sec (x) dx = ln|sec (x) + tan (x)|+ Cġ0.Video, we tried to find the area of the region, I ∫ x ndx = (x n+1/ n+1) + C, when n ≠ −1 Trigonometric Integralsĩ. Related: Definite Integral Properties Frequently Used Indefinite Integrals General and Logarithmic Integralsĥ. Differentiating the result will give you the initial function again. Indefinite Integrals: Calculating indefinite integrals basically gives us the antiderivative of the function.
There are two types of integrals namely definite and indefinite integrals.ĭefinite Integrals: Calculating definite integral consists of a lower and upper bound and we get a number as a result which is basically the area bounded by the graph, lower and upper bounds and the coordinate axes. An integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data.īasically, integration is the same as anti-differentiation or is the reverse process of differentiation. Integration is one of the two main operations of calculus its inverse operation, differentiation, is the other. The antiderivative of the function will be displayed and related graphs will also be displayed. Enter the variable with respect to which the integral has to be calculated in the second column.Ĥ. Enter the function to integrate into the first column.Ģ.
#INTEGRAL GEOMETRY CALCULATOR FREE#
This free online calculator can make it really fast and easy.

We know that integral calculation is a tedious process with a variety of functions to remember and procedures to do. This indefinite integral calculator is a free online tool to evaluate the antiderivative of a function.


 0 kommentar(er)
0 kommentar(er)
